Bisher haben noch nicht untersucht unter welchen Umstaenden ein invarianter (Fix) Punkt auch einen Attraktor darstellt.
Unser Freund y0i ist z.B. fuer alle a ein Fixpunkt.Fuer a <3 auch Attraktor. Fuer a>3 muss er jedoch den ersten periodischen Attraktoren Platz machen. Fixpunkt ist lediglich eine notwendige Bedingung fuer ein Attraktorendasein. Die hinreichende Bedingung ist ueber ein Konvergenzkriterium gegeben.
Das Konvergenzkriterium kann man im Iternet z..b. unter http://www.gus.bb.bw.schule.de/fbaum/fbaum.htm finden.
Wir nennen einen Fixpunkt y*
anziehend, falls | f ´(y*)| < 1
abstoßend, falls | f ´(y*)| > 1
inndifferent, falls | f ´(y*)| = 1
Mit f ´(y*) ist in der Schreibweise hier die Ableitung der Abbildungsfunktion nach den Anfangswerten an der Stelle y=y* gemeint.
Fuer einen nichtperiodischen Attraktor ist dies einfach dp1/dy , y=y*
ACHTUNG ! DIES GILT NICHT FUER PERIODISCHE ATTRAKTOREN !
Betrachtet man z.B. die erste Periodenverdopplung ueber das erste verketteten Polynom p2, so ist dieses zu differenzieren !

BEISPIEL einfacher Fixpunkt y0i

Die Ableitung ist fuer die logistische Gleichung einfach zu berechnen:
p1(y) = a y (1-y) = a y-a y**2 .
|dp1(y)/dy | = |a-2a y | = |a(1-2y)|
Um einen Fixpunkt ! y* z.B. auf "anziehend" zu untersuchen setzt man diesen in |a(1-2y)| ein und ermittelt fuer welche a dieser Ausdruck kleiner eins ist. .

Abb10 zeigt das y0i das Konvergenzkriterium fuer 1<a<3 erfuellt.

Abb.10

Ohne Rechnung: Fuer a<1 ist der Fixpunkt 0 Attraktor.
Fuer den Parameterwert a=2 scheint die logistische Abbildung besonders schnell zu konvergieren.

BEISPIEL : Attraktoren des ersten Zweierzyklus. y2a , y2b
Hier wurden die Schnittpunkte von p2 mit der 45 Grad Linie betrachtet. Es ist also p2 zu differenzieren.Dies ergibt ein Polynom 3 ter Ordnung, in das die Fixpunkte y2a und y2b eingesetzt werden muessen.Bei manueller Rechnung ist dies schon ein groesserer Rechenaufwand.

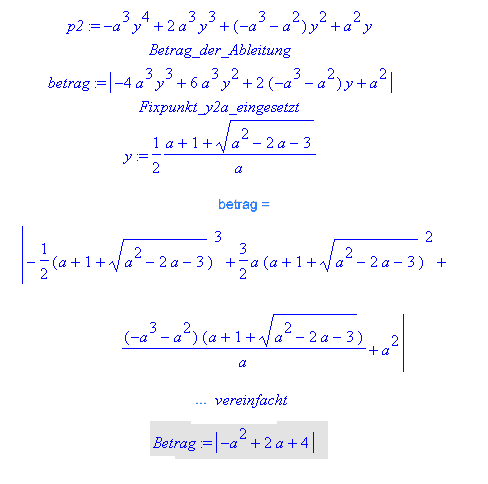
Abb.11 zeigt die Konvergenzbereiche beim 2 er Zyklus

Abb.11

positive Loesungen der Gleichung: |a**2-2a-4| =1 sind 3 und 1+sqrt(6)
positive Loesung der Gleichung: |a**2-2a-4| =0 ist 1+sqrt(5)
Das ist das Doppelte des goldenen Schnittes. Hier scheint der 2 er Zyklus am schnellsten zu konvergieren.
Fuer die Birfurkationsstelle a=3 liegt dagegen eine schlechte Konvergenz vor.

Anmerkung von KONRAD:
*********************************************************************
"Repulsor" heisst ein Punkt, der nur für ganz bestimmte Startwerte den Endzustand darstellt,
z.B. y0i bei a>3 und y2ia,b bei a >3,45 .
Bei allen anderen Werten hingegen tendieren die Werte hin zum Attraktor.
Wobei in den chaotischen Bereiche von einem chaotischen Attraktor die Rede ist.
*********************************************************************
Repulsoren sind also Fixpunkte,die das Konvergenzkriterium nicht erfuellen.
Grafik Zusammenfassung