|
DER LJAPUNOV EXPONENT
|
Der Ljapunovkoeffizient ist wie folgt definiert:
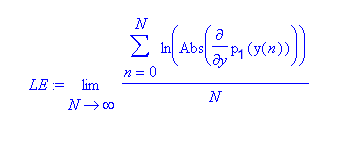
Die Formel erscheint kompliziert, stellet aber lediglich eine
Arbeitsanweisung dar:
DER LJAPUNOV EXPONENT
ist ein einfaches Anzeigegeraet, dass die Ordnung/Unordnung eines Prozesses
numerisch ermittelt:
|
LE<0 Ordnung
|
| LE=0 Birfurkation |
| LE>0 Chaos |
Das Ljapunov Anzeigegeraet erfordert eine weitere Berechnung waehrend
der Iteration. Dazu verwendet man eine Variable
z.B. sp als Summen-Speicher. Aus dem aktuellen Iterationswert yn bildet man
ln(Betrag(dp1(yn)/dy)) und addiert den Wert
in den Speicher sp. dp1/dy waere bei der logistischen Abbildung analytisch zum
Beispiel a-2ay.
Die Summe teilt man dann durch die Anzahl der Iterationen. Den Fall ln(0) muss
man natuerlich ausschliessen.
Programmbeispiel fuer Verhulst Gleichung mit dem Mathematikprogramm
Maple:

Anm: In analytischen Mathematikprogrammen wie Maple oder Derive muessen Pixel
fuer die Grafkausgabe in einem
Feld gespeichert werden. Im Beispiel aa[i] y[i]. Eine raffinierte Methode wie
in solchen Programmen die Berechnung
waeherend der Grafikausgabe durchgefuehrt werden kann, wird hier noch vorgestellt.
Abb 12. zeigt den mit dem Programm ermittelten Ljapunov Exponenten ueber dem Parameter 1<a<4 :
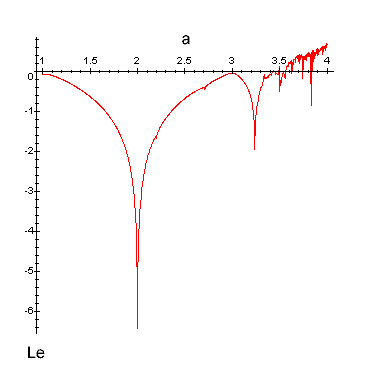 Abb. 12
Abb. 12
Die Gleiche Simulation fuer den Bereich 3.6<a<4 mit 100 Iterationen
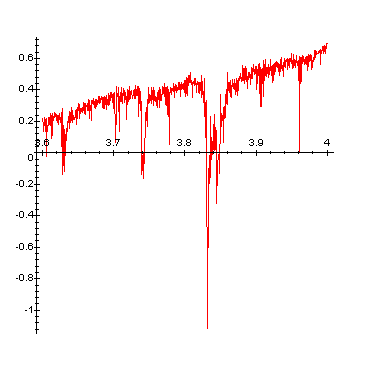
d.t.o mit einem Vorlauf zum Einschwingen von 100 Iterationen

| Hauptmenue | Der Ljapunov Exponent 2 |