ANWENDUNG 1
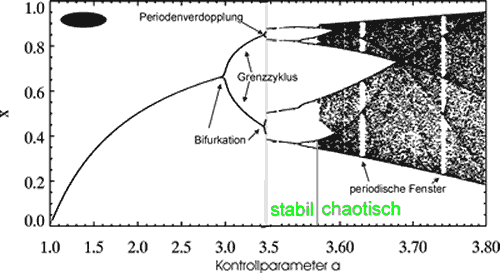
y(k+1)=a*y(k)*(1-y(k))
Das Feigenbaubdiagramm fue a<3
Zu den Grundlagen

Abb5

Das Feigenbaumdigramm (auch Periodendigramm) stellt die Attraktoren der Verhulst Gleichung ueber dem Parameter a graphisch dar. In Abb.5 seher wir, dass die Verhulst Gleichung fuer a<3 gegen einen konstanten Wert konvergiert. Warum ist zunaechst egal. Wir nehmen das einfach mal an. Wir haben dies bereits als y(k+1)=y(k) beschrieben. Das war praktisch, denn so konnnten wir wenigstens einen tapferen invarianten Anfangswert berechnen. y0i=(a-1)/a Wir koennen das auch so beschreiben,dass dieser Wert y0i immer auf sich selbst abgebildet wird. Ueberhaupt kann man sagen, dass wenn die Verhulst Gleichung gegen einen kostanten Wert yc konvergiert, dass dies nur moeglich ist, wenn yc immer wieder auf sich selbst abgebildet wird. Einen solchen Wert habe wir ja schon kennengelernt naemlich yoi.

Kann es fuer a<3 sein , dass es noch irgendeinen Wert gibt, der staendig auf sich selbst abgebildet wird,ausser y=0 und y0i ?

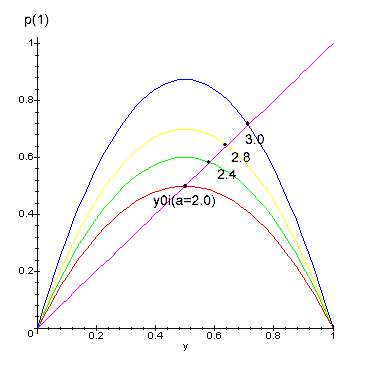Abb.6

Die Antwort ist ganz klar NEIN ! Die 45 Grad Linie in Abb.schneidet die p(1) Verhulst Funktionen immer nur in einem Punkt naemlich y0i ! ( Abgesehen von y=0. )
D.h. wenn die Iteration gegen einen Wert konvergiert so kann dies nur der Wert yoi sein !
Und dieser Wert ist natuerlich unabhaengig vom Anfangswert. D.h. egal welchen Anfangswert ich waehle. Dieser Anfangswert wird zunaechst abgebildet dann gespiegelt, wieder abgebildet ... Falls die Iteration gegen einen Wert konvergiert so kann dies nur yoi sein. yoi zieht gewissermassen alle Punkte an.
yoi ist also ein ATTRAKTOR ! (Anziehend, man denke an attraktiv) Der grosse Anzieher :-)
Und wir haben yoi in Abhaengigkeit von a, also y0i(a) ja sogar schon berechnet !
Damit kennen wir wenigstens fuer a<3 schon den Attraktor.
Jetzt also die erste Anwendung !
Wir koennen sofort das Periodendiagramm fuer a<3 ohne eine einzige Berechnung angeben !
Das Periodendiagramm stell ja die im Computerexperiment ermittelten Attraktoren ueber a dar.
Voila haben wir doch laengst schon berechnet:

Im Bereich a<3 folgt das Feigenbaumdiagramm der Funktion yoi(a)=(a-1)/a

Abb.7

In Abb7 ist die Funktion (a-1)/a rot eingezeichnet.
Voraussetzung wart, dass jeder Anfangswert gegen diesen Attraktor konnvergiert. Das haben wir noch nicht bewiesen. Aber die Einschwingphase, die wir im Computerexperimet fuer das Periodendiagramm benoetige koennenn wir uns doch jetzt auch sehr schoen erklaeren.

ZUSAMMENFASSUNG:


Es gibt fuer a<3 lediglich einen Anfangswert, der staendig auf sich selbst abgebildet wird. Staendig auf sich selbst abgebildet bedeutet der Wert bleibt konstant.
Graphisch bedeutet dies, dass sich hier die Funktion p(y)=a*y*(1-y) und die 45 Grad Linie f(y)=y schneiden. y0i(a) kann man also auch aus p(1)=y berechen. Diese Gleichung hat neben y=0 nur eine Loesung ! Es gibt nur einen Schnittpunkt. => Es gibt nur einen "konstanten" nichtperiodischen Attraktor. FALLS die Anfangswerte gegen einen konstanten Wert konvergieren wie im Fall a<3 so koennen sie nur gegen diesen einzigen ATTRAKTOR yoi(a)=(a-1)/a konvergieren. Dieser Attraktor ist unabhaengig vom Anfangswert !
Im Fall der Periodenverdopplung existiert dieser sich selbst abbildende Punkt immer noch,
aber er stellt keinen Attraktor mehr dar.
Die Iteration der Verhulst Gleichung konvergiert fuer a>3 nicht mehr gegen yoi.
Hauptmenue Anwendung 2