BESCHREIBT DIE VERHULSTGLEICHUNG EINE RAUPENPOLULATION ?
***************************************************************************************
Die Verhulstgleichung ist eine Differenzengleichung, die kontinuierliche und
keine diskretisierten Ausgangsgroessen betrachtet.
Die Anzahl der Raupen einer Population wird jedoch durch natuerliche Zahlen
beschrieben. Es gibt keine halben Raupern.
Nun koennte man meinen, dass die diskrete Form der Verhulst Gleichung gegen
die kontinuierliche Form konvergiert.
Numerische Versuche zeigen hierbei jedoch ein anderes Ergebnis :
Eine wertediskrete Form der Verhulst Gleichung laesst sich ueber die floor()
oder ceil() Funktion formulieren :
y[i]:=floor{a/Pop_max*y[i-1]*(Pop_max-y[i-1])}
y[i]:=ceil{a/Pop_max*y[i-1]*(Pop_max-y[i-1])}
Pop_max ist dabei die maximale Anzahl Induvidien einer Population :
Zur Veranschaulichung die Uebertragungsfunktionen der Verhulst Gleichung fuer
a=4,Pop_max=10 :
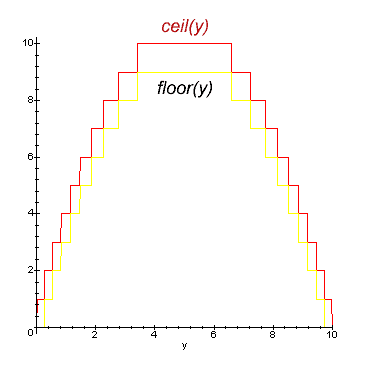
Beobachtung beim numerischen Experiment :
*************************************************
Benutzt man die ceil() Funktion und den Parameter a=4, so kann die Population
spontan "aussterben" Das ist verstaendlich,
denn die Funktion kann y[i] nach pop_max runden und im naechsten Schritt bedeutet
dies das Ende der Population.
Mit der floor(y) Funktion laesst sich dies vermeiden
Der Parameter a=4 fuehrt in der "analogen" Verhulst Gleichung zu chaotischem
Verhalten. In der diophantischen floor Variante
ist dies nicht der Fall ! Erst bei einer genuegend hoher Anzahl von natuerlichen
Zahlen tritt chaotisches Verhalten auf.
Systematisches Erfassen.
*******************************
Der Grad von Ordnung-Unordung, Chaos, Zufall laesst sich ueber den Ljapunov
Exponenten bestimmen.
Ueblicherweise wird dieser ueber den Parameter a dargestellt.
Im folgenden habe ich diesen ueber die maximale Populationsgroesse pop_max und
a=4 dargestellt.
Anmerkung:
**********
Den Ljapunovexponenten (also unser Zufallsanzeigegeraet) kann man innerhalb
der Simulation numerisch bestimmen.
Dabei muss jedoch die Ableitung der Uebertragungsfunktion analytisch bekannt
sein.
Man muesste aufgrund der unstetigen floor() Funktion hier die Distributionentheorie
anwenden.
Darauf habe ich in der folgenden Darstellung verzichtet. Diese ist daher noch
fehlerhaft, aber dennoch bereits recht interessant.
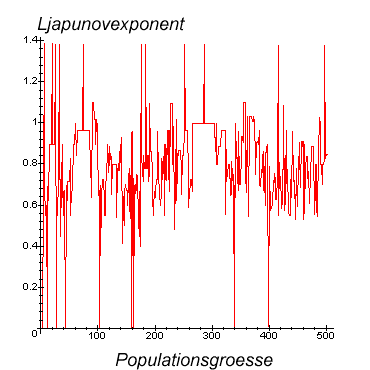
Die Erwartung, dass der Ljapunovexponent gegen den nichtdiskreten Fall konvergiert
erfuellt sich nicht.
Numerisch ermittelter Ljapunov Exponent fuer die diskrete Verhulst Gleichung
*******************************************************************************************
Um die Beruecksichtigung von Distributionen im diskreten Fall zu umgehen habe
ich im folgenden den numerisch ermittelten
Ljapunov Exponenten verwendet. Damit umgeht man die analytische Differentation
der unstetigen Uebertragungsfunktion.
Einen numerischen Algorithmus dazu habe ich auf dieser Webseite bereits hier
hergeleitet.
Der Algo ist 1.Ordnung und damit auch keine sonderlich exakte Approximation.
Vergleich der beiden Verfahren :

In der numerischen Simulation ist ein Vorlauf von 50 Iterationen implementiert.
a=4. Fuer jeden Parameter Pop_max
wurden 200 Iterationen verwendet.
rot=Ljapunov ohne Beachtung der Distributionen.
Die gruene Kurve stellt die rein numerische Approximation des Ljapunovexponenten
dar. Es gibt deutliche Abweichungen.
Die Paeks gegen Null sind interessant.
Hier tritt in dem Bereich, der im kontinuierlichen Fall Chaos darstelllen wuerde,
eine Ordnung (Periodizitaet) auf.
Im folgenden numerischen Experiment wurde die Diskretisierung nun von 2-100
Werte auf
200 000 - 1 000 000 Werte schliesslich auf 10 000 000 Werte erhoeht. a=4 :
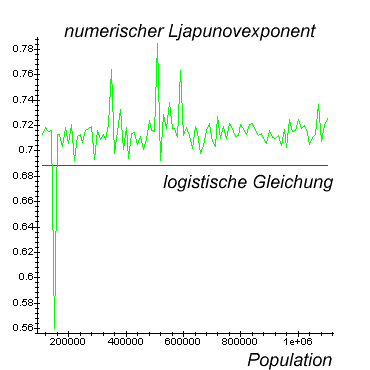
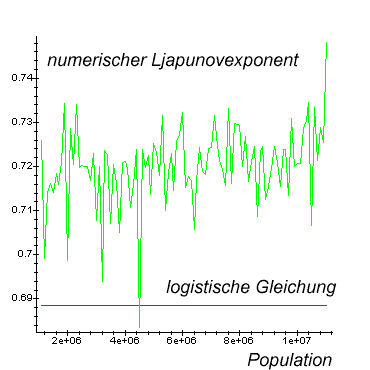
(Bitte die Skalierung beachten) Der Ljapunov Exponent liegt nun im Bereich des
kontinuierlichen Wertes. Man koennte eine
Konvergenz annehmen. Allerdings sieht man, dass immer noch Peaks in Richtung
einer Birfukation auftreten.
Es waere interessant zu untersuchen, ob solche speziellen Populationsgroessen,
Fenster der Ordnung, tatsaechlich auftreten.
Letztendlich sind diese darin begruendet, dass die Popolationsgreoesse den Parameter
a des nichtdiskreten Falls veraendert.
y[i]:=floor{a/Pop_max*y[i-1]*(Pop_max-y[i-1])}
Nov 2006 / Jan 2010




