Kompakte Darstelllung eines Binaerbaumes in der komplexen Ebene

ANWENDUNG :

Binaerer Phasomat

Es zeigt sich, dass bei einer Berechnung ueber vele Iterationsschritte die Wahl des Vorzeichens, des Zweiges, eine entscheidende Rolle spielt. Waehlt man das Vorzeichen rein zufaellig, so nimmt der komplexe Funktionswert Werte an, die alle Bereiche des Kreises recht gleichmaessig enthalten.
Die folgende Abbildung zeigt das Ergebnis fuer 500 Iterationen bei denen das Vorzeichen der Wurzel zufaellig gewaehlt wurde :

Waehlt man das Vorzeichen dagegen determiniert liegen die Iterationswerte auf beschraenkten Bereichen des Einheitskreises. Im folgenden Bild wurde das Vorzeichen bei 500 Iterationsschritten determiniert, abwechselnd positiv und negativ gewaehlt :

Waehlt man das Vorzeichen fuer einen bestimmten Durchlauf des Entscheidungsbaumes zufaellig, ergibt sich somit ein aehnliches Bild wie wenn man alle Wege des Entscheidungsbaumes durchlaeuft. Das ist keinesfalls zu erwarten. Man koennte hier auch von einer Ergodizitaet sprechen. Damit laesst sich der Binaerbaum verwenden um Zeitreihen hinsichtlich ihrer Zufaelligkeit zu untersuchen. Indem man diese fuer die Auswahl des Loesungszweiges (Steuerung des Vorzeichens) heranzieht.
Spaeter wird eine Methode vorgestellt bei der die zu untersuchende Funktion nicht nur auf binaere Zeichen beschraenkt ist.

MAPLE-QUELLCODE fuer die beiden Abbildungen :
(Maple rechnet immer komplex)

restart; with(plots):randomize;
z0:=1;N:=500;
wahl:=rand(0..1);
for i from 1 to N do
#if (i mod 2 =0 ) then # Determinierte Wahl (auskommentiert)
if (wahl()=0 ) then # Zufaellige Wahl
z[i]:=evalf(sqrt(z0));z0:=z[i];
else
z[i]:=evalf(-sqrt(z0));z0:=z[i];
fi;
od:
druck:=seq(z[i],i=1..N):
complexplot ([druck],x=-1..1,style=point);

MAPLE-QUELLCODE, der die Steuerbits aus einem String liest :

bits:=`111011110111110000000001100000011111000`;
z0:=1;
N:=length(bits);
for i from 1 to N do
if substring(bits,i)=`1`then;
z[i]:=evalf(sqrt(z0));z0:=z[i];
else
z[i]:=evalf(-sqrt(z0));z0:=z[i];
fi;
od;
druck:=seq(z[i],i=1..N):
complexplot ([druck],x=-1..1,style=point);

(Der evalf Befehl ist notwendig um die Rechenzeit zu beschleunigen)

Kreisring-> Kreisscheibe
*********************
Um die zeitliche Abhaengigkeit in die Darstellung mit einzubringen kann man den Radius als Zeit / Iterationskoordinate verwenden. Man stellt somit i*z[i] dar. Da die Kreisflaeche quadratisch mit dem Radius steigt : sqrt(i)*z[i].

Beispiel :
Rabbit Sequenz :

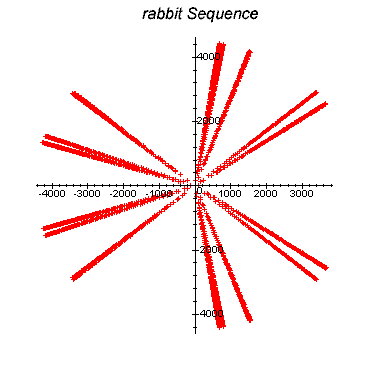
Wie man sieht ist die Rabbit Sequenz keinesfalls ein reiner Zufallsprozess. Bei einem Zufallsprozess egibt sich folgendes Bild :

Zur Erinnerung. Das Bild wird durch einen einzigen Weg durch den Binaerbaum erzeugt. Und dennoch werden dabei fast alle moeglichen Zustaende "besucht".

PHASOMAT fuer Dezimalziffern
*******************************
Die Wahl von "plus" oder "minus" war eine binaere Wahl. Jetzt basteln wir eine Entscheidungsstelle mit 10 Ausgaengen,
die ueber die Ziffern 0..9 angesteuert werden. Also ein dezimaler Entscheidungsbaum. Die Gleichung z^p-z0=0 hat p Loesungen : z = z^(1/p) alle p Werte. Sie ist p fach mehrdeutig. Ansonsten ist die Vorgehensweise wie beim Binaerbaum. und man kann sofort das Ergebnis der binaeren Rechnung uebernehmen :

z=exp(1/p*(ln|z]+I*arg(z)/p+I*2*k*PI/p), k=0..p

arg(z) ist der arctan(z) wobei man die Quadranten beachten muss. Wir verwenden als Startwert z0=1. Der Betrag bleibt immer gleich, daher die Vereinfachung ln|z|=0

Maplecode :
*********

grad:=10;
st die (zufaellige) Steuervariable 0..9
z[i]:=evalf(exp(I*(argument(z0)+2*st*Pi)/grad));
z0:=z[i]; grad:=10;

Kompletter Beispiel Code : (Ziffern der Dezimalzahlen)
********************
restart; with(plots):
bits:=`102345678910111213141516171819202122232425262728293031323334353637383940
41424344454647484950515253545556575859606162636465666768697071727374757677787
980818283848586878889909192939495969798991001011021031041051061071081091101111
121131141151161171181191201211221231241251261271281291301311321331341351361371
381391401411421431441451461471481491501511521531541551561571581591601611621631
641651661671681691701711721731741751761771781791801811821831841851861871881891
901911921931941951961971981992002012022032042052062072082092102112122132142152
1621721821922022122222322422522622722822923023123`:
randomize;
grad:=10;
z0:=1;
phi0:=0;
Digits:=20;
N:=length(bits);
#N:=50;
# wahl:=rand(0..9); RND GENERATOR IST DEAKTIVIERT
rr:=1;
for i from 1 to N do
st:=99;
ch:=substring(bits,i);
if ch=`0`then st:=0;fi;
if ch=`1`then st:=1;fi;
if ch=`2`then st:=2;fi;
if ch=`3`then st:=3;fi;
if ch=`4`then st:=4; fi;
if ch=`5`then st:=5;fi;
if ch=`6`then st:=6;fi;
if ch=`7`then st:=7;fi;
if ch=`8`then st:=8;fi;
if ch=`9`then st:=9;fi;
# st:=wahl();
if st<>99 then z[rr]:=evalf(exp(I*( argument(z0)+2*st*Pi )/grad) );
z0:=z[rr];
rr:=rr+1;
fi;
od:
N:=rr-1;

druck:=seq(sqrt(i)*z[i],i=1..N):
complexplot ([druck],style=point,symbol=DIAMOND,color=black);

Ausdruck :

Die Spiralarme verkoerpern die Ziffern 1...9

PHASOMAT fuer ASCII Zeichen
********************************
Um Texte beurteilen zu koennen kann das selbe Prinzip angewendet werde. Man benoetigt fuer das Alphabet nun eine 26-deutige Uebertragungsfunktion. Die 26 te Wurzel der komplexen Zahl eins:

Programmbeispiel
**************
restart; with(plots):
bits:=`Geben sie hier den zu analysierenden Text ein`:
grad:=26;
z0:=1;
N:=length(bits);
ii:=1;
for i from 1 to N do
st:=99:
ch:=substring(bits,i):
if (ch=`A` or ch=`a` or ch=`Ä` or ch=`ä`) then st:=0; fi;
if (ch=`B` or ch=`b`) then st:=1; fi;
if (ch=`C` or ch=`c`) then st:=2; fi;
if (ch=`D` or ch=`d`) then st:=3; fi;
if (ch=`E` or ch=`e`) then st:=4; fi;
if (ch=`F` or ch=`f`) then st:=5; fi;
if (ch=`G` or ch=`g`) then st:=6; fi;
if (ch=`H` or ch=`h`) then st:=7; fi;
if (ch=`I` or ch=`i`) then st:=8; fi;
if (ch=`J` or ch=`j`) then st:=9; fi;
if (ch=`K` or ch=`k`) then st:=10; fi;
if (ch=`L` or ch=`l`) then st:=11; fi;
if (ch=`M` or ch=`m`) then st:=12; fi;
if (ch=`N` or ch=`n`) then st:=13; fi;
if (ch=`O` or ch=`o` or ch=`Ö` or ch=`ö`) then st:=14; fi;
if (ch=`P` or ch=`p`) then st:=15; fi;
if (ch=`Q` or ch=`q`) then st:=16; fi;
if (ch=`R` or ch=`r`) then st:=17; fi;
if (ch=`S` or ch=`s`) then st:=18; fi;
if (ch=`T` or ch=`t`) then st:=19; fi;
if (ch=`U` or ch=`u` or ch=`Ü` or ch=`ü`) then st:=20; fi;
if (ch=`V` or ch=`v`) then st:=21; fi;
if (ch=`W` or ch=`w`) then st:=22; fi;
if (ch=`X` or ch=`x`) then st:=23; fi;
if (ch=`Y` or ch=`y`) then st:=24; fi;
if (ch=`Z` or ch=`z`) then st:=25; fi;

if st<>99 then
z[ii]:=evalf(exp(I*(argument(z0)+2*st*Pi)/grad));
z0:=z[ii];
ii:=ii+1;
fi;
od:
N:=ii-1;
druck:=seq(i*z[i]/N,i=1..N):
complexplot ([druck],style=point);

Beispiel eines laengeren Textes :

Die besonders dicht belegten Sektoren stellen die Vokale a e i o u dar.

Besonderheiten :

Tritt z.B. bei einer Kodierung der Zahlen 0...9 eine Ziffer im Teststring nicht auf, so ergibt sich nicht nur ein leerer Sektor, sonder selbstaehnliche Nebenstreifen :

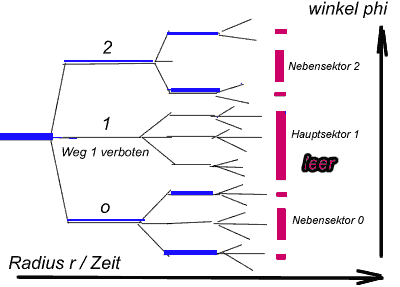
Erklaerung fuer die Nebensektoren :
Was bedeutet ein Sektor ?
Das sind Werte mit dem selben Argumentintervall. Und da wir in der Darstellung nun den Betrag zeitlich kuenstlich stetig
erhoehen i*z[i] steht ein Sektor auch fuer den gleichen Betrag. (Der Radius des Kreises ist die Zeitachse.) Ein freier Sektor
steht somit fuer einen zusammenhaengenden Bereich aller Entscheidungsergebnisse, die man nicht erreicht hat.

Folgende Grafik erlautert den Zusammenhang :


In der Phas- O- Mat Galerie sind zahlreiche Versuche mit der Methode dargestellt.
Link zur Galerie bei quanten.de