************************
Als einfache binaere Verzweigung eignet sich die Funkti f(x)=y=x^2 Die Umkehrfunktion lautet x=+/-Wurzel(y). Die Unkehrfunktion ist somit zweideutigund. Das Vorzeichen +/- entspricht einer binaeren Codierung der Verzweigung.

Kompakte Darstelllung eines Binaerbaumes in der komplexen Ebene
ZIEL :
Es soll ein (binaerer) reeller Entscheidungsbaum moeglichst einfach und kompakt
dargestellt werden.
Es wird sich zeigen, dass die erarbeitete Methode in der Lage ist Binaerbaueme
mit unendlich vielen Verzweigungen darzustellen.. Ebenso laesst sich das Verfahren
zur Beurteilung von Zufallsprozessen einsetzen.
Beispiel eines binaeren Entscheidungsbaumes
**********************************
........................................____11____ Pizzeria
......................____1____|___10____ Schuhgeschaeft
.__________|
.................... |____0________01____ Autobahn
.........................................|___00____ Fitnesscenter
Die Linien sollen Strassen darstellen. Es existiert auf jeder Strasse eine
Abzweigung, Bifurkation. Jedes Ziel laesst sich damit binaer codieren. In der
Form welcher Weg bei jeder Abzweigung verwendet wurde.
Trick zur Kompaktifizierung der Darstellung :
A) Die Kreuzungen sollen ueber eine nichtbijektive Abbildung beschrieben werden
B) Das durchlaufen von n Kreuzungen soll durch n Iterationen dieser Abbildung
beschrieben werden
C) Die Zustaende sollen auf dem Einheitskreis in der komplexen Ebene abgebildet
werden
A) Die nichtbijektive Abbildung
************************
Als einfache binaere Verzweigung eignet sich die Funkti f(x)=y=x^2 Die Umkehrfunktion
lautet x=+/-Wurzel(y). Die Unkehrfunktion ist somit zweideutigund. Das Vorzeichen
+/- entspricht einer binaeren Codierung der Verzweigung.

B) Die iterative Abbildung
********************
Alleine die Funktion +/-Wurzel(y) als Loesung ist weniger interessant, dann
sie codiert nur 1 Bit. Fuehrt man die Abbildung n mal iterativ aus, so ergeben
sich 2^n Loesungen. Ein Loesungsbaum.
Beispiel :
f(n+1)=f(n)^2, f(0)=f0
f(n+2)=f(n+1)^2=(f(n^2))^2=f(n)^4
Die Iteration vekettet die Abbildungsfunktion und dementsprechend lautet die
Loesung der DZGL eindeutig :
1) f(n)=f0^(2^n)
**************
Eine eindeutige Abbildung interessiert uns nicht. Daher betrachten wir die mehrdeutige
Umkehrabbildung :
f(n+1)=+-Wurzel(f(n)=+-f(n)^(1/2), f(0)=f0
f(n)=f0^(1/2^n) ist somit nur eine Loesung von 2^n Loesungszweigen. Insbesonders
sieht man, dass man die Loesung um die komplexen Zahlen erweitern muss. Man
muss somit von anfang an komplexwertig rechnen :
2) z(n+1)=+-z(n)^(1/2), z(0)=z0
**************************
Es waere falsch zu sagen z(n)=z0^(1/2^n) waere die Loesung, denn ein Polynom
vom Grad 2^n weist 2^n Loesungen auf.
C) Die komplexwertige geschlossene Loesung der Iteration
*********************************************
Einen besonders einfachen Fall erhaelt man wenn man fuer z0 eine Zahl waehlt
mit |z(0)|=1. Also auch einfach z(0)=1
Da die Iteration am Betrag nichts aendert liegen alle Iterationswerte dann auf
dem komplexen Einheitskreis :
1) z(n+1)=z(n)^(2)
2) z(n+1)=+-z(n)^(1/2), z(0)=1
Einige Werte :
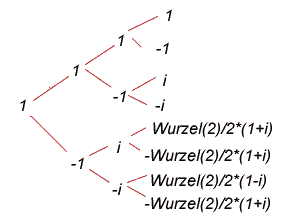
Man kann die Werte auch ueber die Fragestellung erhalten, welche Werte ueber
die Umkehrfunktion auf z0=1 abgebildet werden :
z^(2^n)=z0(alle 2^n Loesungen sind zu bestimmen)
wobei nicht nur der Hauptwert zu betrachten ist :
Ein Hilfsmittel dafuer ist der komplexwertiger Logarithmus:
![]()
LOESUNG VON z^(2^n =z0
***********************
=>
z=z0^(1/2^n)
Wir bilden fuer z=z0^(1/2^n) auf der rechten Seite exp(ln(...))
z=exp(ln (z0)^(0.5^n) ) => LOGARITHMENGESETZ
z=exp(0.5^n*ln(z0)) => KOMPLEXWERTIGER LOGARITHMUS
z=exp(0.5^n*(ln|z0|+i*(arg(z0) + 2*k*Pi) ) k element Z => LOGARITHMENGESETZ
z=|z0|^(1/2^n)*exp(i*(arg(z0) + 2*k*Pi)/2^n ) k element Z
*********************************************
Der einfache Fall fuer z0=1
z=exp(i*2*k*Pi/2^n ) k element Z
**************************
Die Loesungen liegen auf dem Einheitskreis, wobei die n-te Loesung den Einheitskreis
ueber 2^n Punkte gleichmaessig teilt.
Darstellung von 16 Loesungen auf dem Einheitskreis :
ABBILDUNG A

Interpretation der 16 Loesungen :
*************************
Folgende Grafik zeigt den aequivalenten Binaerbaum zu der obigen Darstellung
:
ABBILDUNG B)
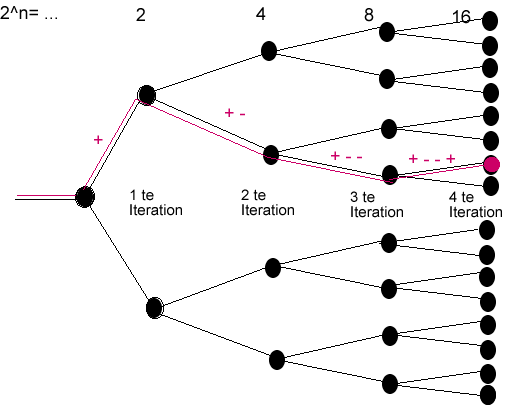
Fuer die 16 Loesungen wurden somit 4 Iterationen, Verzweigungen durchlaufen.
Jeder Punkt des Binaerbaumes wurde eindeutig auf den Einheitskreis der komplexen
Ebene abgebildet. Aus dem Phasenwinkel arg in Abb A und der Bedingung |z|=1
laesst sich somit endeutig bestimmen welches Vorzeichen (Kodierungszeichen)
gewaehlt wurde und sukzessive die komplette Kodierung. In Abb B ist ein einzelner
Weg (rot) plus Kodierung dargestellt. Jedem komplexen Wert in Abb A entspricht
somit auch eine eindeutige Kodierung, Information. Keine der Loesungspunkte
in Abbildung A liegen uebereinander , denn der Kreis wird ja in 2^n Winkel eingeteilt.
Damit laesst sich auf diesem unendlich viele Verzweigungen darstellen.
Beipiel :
Fuer 20 Iterationen, Verzweigungen ergeben sich schon ueber eine Million Aeste.
Diese wuerden dann natuerlich auch den kompletten Einheitskreis fuellen. Die
Darstellung soll daher auch nicht in dieser Form verwendet werden, sondern als
ein Hilfsmittel um Zufalssprozesse grafisch zu beurteilen. Hiebei wird die Ergodenhypothese
eine Rolle spielen.