Schnelle rein algebraische Loesung der VDZGL fuer r= 2, r=4
*****************************************************

Allgemeine Formulierung zur Loesbarkeit spezieller quadratischer Differenzengleichungen

Jede Differenzengleichung der Form

y[k+1]=(p+q*y[k])^2

oder

y[k+1]=2*(p+q*y[k])^2-1

laesst sich mit folgender Substitution T1 so "zentrieren"

T1 : y[k]=(z[k]-p)/q

dass sie mittels einer zweiten nichtlinearen Substitution T2 loesbar ist

Beispiel VDZGL:
***********
Die Verhulst DZGL laesst sich durch folgende Substitution zentrieren :
x(k)=1/2*(1-z(k))

MAPLECODE ALS TEST
restart;
g:=x1=2*x0*(1-x0);
x1:=(1-z1)/2;
x0:=(1-z0)/2;
solve(g,z1);

und mittels x(k)=(1-2*z(k)) wieder Ruecktransformoeren

MAPLECODE ALS TEST
restart;
g:=x1=x0^2;
x1:=(1-2*z1);
x0:=(1-2*z0);
solve(g,z1);

Graphische Veranschaulichung von T1 :
*****************************
Die Transformation z[k]=p+q*y[k] entspricht einer linearen Verschiebung der Polynome :
Beispiel der ueberT1 : z[k]=1-2*y[k] verschobenen Verhulst Polynome :
Ausgangspolynome :

Transformation T1, Lineare Verschiebung


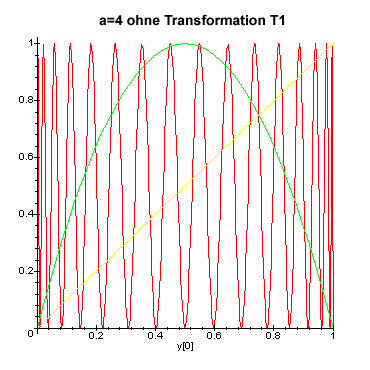
Transformation T1, Lineare Verschiebung

Feigenbaumdiagramm der verschobenen, zentrierten Verhulstgleichung


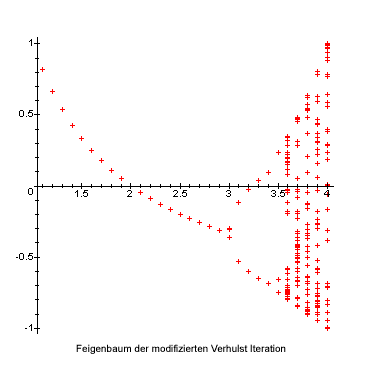
Konkrete Rechnung :
****************

Ausgangsgleichung y(k+1)=2*y(k+1)*(1-y(k) )
***********************************
Umformen zur (bekannten) Zielsubstitution

y(k+1)=2*y(k+1)-2*y(k)^2
2*y(k+1)=4*y(k+1)-4*y(k)^2
1-2*y(k+1)=1-4*y(k+1)+4*y(k)^2
1-2*y(k+1)=(1-2*y(k))^2
ln(1-2*y(k+1))=2*ln(1-2*y(k))

Zielsubstitution :
(allgemein g{y[k+1]}/g{y[k]}=konstant
Das ist der wichtigste Punkt bei dieser DZGL

ln(1-2*y(k+1))
----------------- =2
ln(1-2*y(k))

Substitution :
z(k)=ln(1-2*y(k))
z(k+1)=2*z(k)

Loesung :
*******
z(k)=z0*2^k =>

Loesung Ruecksubstitution
ln(1-2*y(k))=ln(1-2*y0)*(2^k)
ln(1-2*y(k))=ln((1-2*y0)^(2^k))
(1-2*y(k))=(1-2*y0)^(2^k)

y(k)=1/2*(1-(1-2*y0)^(2^k))
***********************

Fuer den chaotischen Fall r=4 lautet die Zielsubstitution

arccos(1-2*y(k+1))
----------------------- =2
arccos(1-2*y(k))

Die geschlossene Loesung der DZGL y(k+1)=4*y(k)*(1-y(k)) lautet somit :

y(k)):=1/2*(1-cos(2^k*arccos(1-2*yx0)))
*************** ******************+

Die Iterationsfolge erscheint uns voellig zufaellig, chaotisch. Es ist allgemein nicht bekannt dass ueberhaupt eine Loesung existiert. Dass die Folge chaotisch sei, wird man darin bestaetigt sehen, dass der Ljapunovexponent hier groesser Null ist. Sogar maximal fuer die Parameter 1..4. Was hier wirklich ablaeuft sieht man jedoch in dieser Grafik .

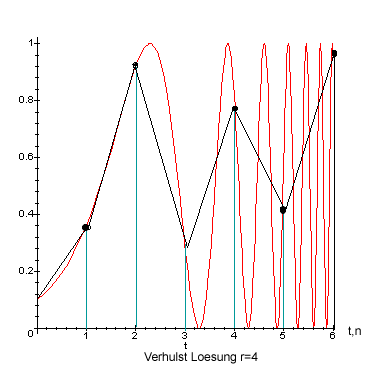
Das Chaos basiert auf einer Kosinusschwingung, deren Frequenz ueber den Term 2^k stetig anwaechst. Nach wenigen Iterationsschritten auf riesige Werte. Die Schwingung wird aequidistant abgetastet und darauf basieren die zufaelligen Werte. Der Ljapunovexponent kann dies nicht wiedergeben. Rein formal habe ich diesen durch eine Modifikation ersetzt in der statt dem ln der arccos bzw arcsin verwendet wird.


Diese Vorgehensweise muesste man sich aber nochmals genauer ueberlegen. Fuer r=1+Wurzel(8) koennte eine aehnliche Loesung wie fuer r=4 existieren.

(2010)